Kỹ thuật sửa lỗi Reed - Solomon

Đây là bài viết thuộc chủ đề nghiên cứu của nhóm ruby hardcore, được lược dịch chủ yếu từ bài viết này.

Background

Là người dùng cuối, chúng ta đã quá quen thuộc với việc click vào nút download A, quét một mã vạch B hay mua một cái đĩa CD C, thì chúng ta đều nhận được một kết quả thích hợp và đầy đủ dữ liệu. Hầu như tải về là cài đặt được, quét mã qr là hiện ra thông tin được, mua đĩa CD về là nghe được, vân vân… Nhưng hậu trường đằng sau của những sự tưởng như bình thường đó không hề bình thường chút nào, vì mọi thứ trên đời đều có khả năng phát sinh lỗi. Và làm sao có thể hạn chế tối đã những lỗi này, thậm chí ưu việt hơn là phát hiện ra lỗi và tự sửa nó, là một vấn đề rất khó.

Reed-solomon là một kỹ thuật trong rất nhiều kỹ thuật nhằm đảm bảo toàn vẹn dữ liệu. Nó cho phép phát hiện và sửa lỗi, được ứng dụng rất rộng rãi, từ những sản phẩm rất bình dân mà bạn thấy hằng ngày như đĩa CD, DVD, cao cấp hơn tí có mã QR, hay các công nghệ phức tạp như DSL, WiMAX, RAID 6, thậm chí cả công nghệ vũ trụ…

Tưởng tượng một chút là ta mua cái đĩa về, mở lên thấy Ưng Hoàng Phúc hát mà thỉnh thoảng lại thấy giọng của Ngọc Trinh thì hay nhỉ :D

Nguyên lý chung

Cứ tưởng tượng thế này cho dễ. Trong 1 đoàn quân gửi đi đánh nhau, rất có thể có những người lính biến chất dọc đường. Làm sao để phát hiện và khôi phục lòng trung thành của những người lính này, thì bạn phải cài cắm người mà bạn tin vào trong đoàn quân đó, để chúng giám sát và báo lại cho bạn nếu có việc trên. Xịn hơn nữa, người được cài cắm có thể tự động khuyên nhủ mấy anh lính hư kia, đưa đoàn quân trở lại sự trung thành nhất, ko còn tạp chất.

Tư tưởng của kỹ thuật Reed-Solomon cũng vậy. Khi bạn gửi một số bit trên đường truyền (=gửi quân đi đánh), rất có thể có những bit bị sai lệch vì nhiễu trên kênh truyền (=lính biến chất), bạn sẽ phải đưa thêm những bit giám sát (=cài cắm người mà bạn tin) vào số bit trên, và truyền tải đi.

Việc cài cắm sẽ được thông qua bộ encoder, và bộ decoder sẽ lo việc khôi phục.

Các khái niệm kỹ thuật liên quan

Theo định nghĩa xịn ở đây:

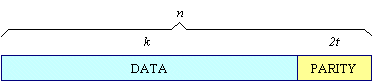
A Reed-Solomon code is specified as RS(n,k) with s-bit symbols.

This means that the encoder takes k data symbols of s bits each and adds parity symbols to make an n symbol codeword.
There are n-k parity symbols of s bits each. A Reed-Solomon decoder can correct up to t symbols that contain errors in a codeword, where 2t = n-k.

Vietsub:

Mã Reed-Solomon được đặc tả là RS(n,k), với mỗi ký tự được cấu tạo từ s-bit.
Nghĩa là bộ mã hóa sẽ nhận k ký tự, sau đó thêm vào các ký tự kiểm tra để tạo ra codeword có độ lớn n ký tự.
Số ký tự kiểm tra là `n-k`, và số ký tự có thể được sửa tối đa là (n-k)/2

Ta có thể liên tưởng đến các khái niệm được nhắc tới với nguyên lý chung ở trên như sau:

symbols(ký tự): Có ý nghĩa như một anh lính. Anh lính này (symbol) được cấu tạo từ s-bit.
k data symbols: Có ý nghĩa như một đoàn quân trước khi được cài cắm người vào. Đoàn quân này có số lượng là k anh lính.
n symbol codeword: Có ý nghĩa như đoàn quân sau khi cài cắm người vào, có số lượng là n anh lính. (n > k)
n-k parity symbols(ký tự kiểm tra): Số lính mà ta cài cắm vào đoàn quân. Tất nhiên mỗi anh lính được cài vào vẫn được cấu tạo từ s-bit.
2t = n-k: Reed-Solomon có thể sửa được tối đa t anh lính (symbols) biến chất trong đoàn quân, với 2t = n - k

Người ta bảo trăm nghe ko bằng một thấy, vậy dưới đây là hơn 100 lần nghe :v

Hình minh họa cấu tạo RS codeword

Một số tính chất

Với một ký tự(symbol) được tạo nên từ s-bit, thì codeword n có độ dài ko quá $n=2^{s}\; -\; 1$ Ví dụ một ký tự có độ dài 8 bit (s=8) thì n <= 2^8 -1 = 255. Một mã RS điển hình là RS(255,223), ta sẽ có: n = 255, k = 223, s = 8, 2t = 32, t = 16
Một symbol được coi là bị lỗi nếu 1 bit trong nó là lỗi hoặc tất cả các bit trong symbol đó là lỗi. Như vậy, với ví dụ cho RS(255,223) ở trên, mã RS này có thể sửa được 16 symbol lỗi (t=16).

Trong trường hợp xấu nhất, có 16 symbol riêng biệt nhau bị lỗi, và chỉ lỗi có 1 bit thôi. Lúc này, bộ giải mã chỉ có thể sửa được 16 * 1 = 16 bit lỗi.
Nhưng nếu như tất cả bit của cả 16 symbol đều lỗi, thì bộ decoder có thể sửa tới 16 * 8 = 128 bit lỗi. Vậy dễ nhận thấy là mã RS sẽ rất đắc lực trong trường hợp mà chuỗi các bit liên tiếp nhau bị lỗi.

Một symbol được coi là bị xóa nếu như biết được vị trí của symbol bị xóa. Bộ decoder có thể sửa được tối đa t symbol lỗi và 2t symbol bị xóa. Khi dữ liệu đi qua bộ decoder sẽ có 3 trường hợp xảy ra:

2e + r < 2t với e là số symbol lỗi, r là số symbol bị xóa, thì codeword n luôn đc bảo đảm là đúng.
Ngược lại, decoder sẽ báo là không thể khôi phục dữ liệu, hoặc:
decoder sẽ decode và khôi phục sai dữ liệu. Đây là trường hợp khi mà chính parity symbols mà chúng ta thêm vào bị lỗi trong quá trình truyền tải. (Đến người mình tin yêu còn phản mình thì có mà bấu víu vào trời :v)

Cài đặt cụ thể

Phần này rất dài, và đặc toán là toán, bạn nào dễ bị đau đầu thì ko nên đọc. Còn bạn nào đầu cứng thì có thể tham khảo ở link:

2 ví dụ trên tác giả viết rõ cho trường hợp áp dụng cho QR code, cũng như giải thích cặn kẽ các kiến thức toán học liên quan, rất đáng tham khảo nếu đi sâu vào tìm hiểu QR.

‎Một số kết luận tóm gọn

Cost càng ngày càng tăng nếu data càng dài (hiển nhiên luôn)
Encoding đã khó, decoding còn khó hơn nhiều :v
Rất nhiều kiến thức toán cao cấp của năm 1 2 đại học được áp dụng như Vành đa thức (univariate polynomials), tập hữu hạn và các phép toán trên tập hữu hạn (finite fields)

PS: trên ruby cũng có lib generate string sang QR code với format png, ansi… mà mình cũng đang sử dụng cho Anychat